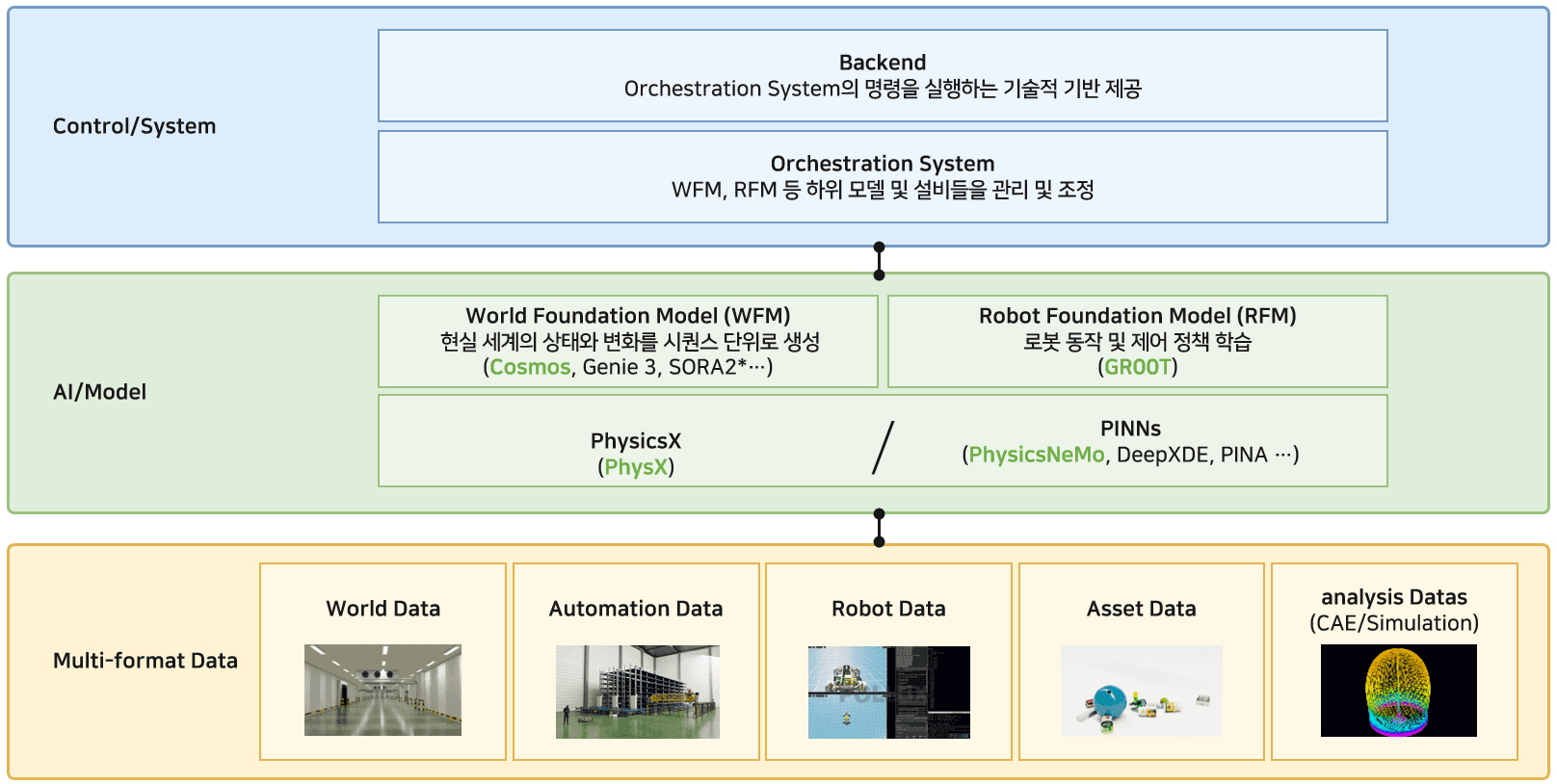
PINNs(Physics-Informed Neural Networks) at a Glance

PINNs (Physics-Informed Neural Networks) are

analytical neural networks embedded with physical constraints,

the World Model is a

representation model that compresses and predicts the dynamics of an environment,

and the Robot Foundation Model is a

large-scale action model integrating perception and behavior.

1. Overall Relationship and Data Flow

┌───────────────────────────────────────────────┐
│ Physics Layer (PINNs) │
│───────────────────────────────────────────────│
│ • Embedding physical equations (PDEs, BCs) │
│ • Learning continuous solution functions │
│ • Generating physics-consistent synthetic data│
└──────────────┬────────────────────────────────┘
│ Providing physically consistent data
▼
┌───────────────────────────────────────────────────┐
│ Cognitive Layer (World Foundation Model) │
│───────────────────────────────────────────────────│
│ • Latent representation of environmental dynamics │
│ • Counterfactual prediction / imagined worlds │
│ • Learning world models based on physics │
└──────────────┬────────────────────────────────────┘
│ Providing simulated environments
▼
┌─────────────────────────────────────────────────┐
│ Behavioral Layer (Robot Foundation Model) │
│─────────────────────────────────────────────────│
│ • Integrated learning of vision/language/action │
│ • Learning generalized behavior policies │
│ • Transfer of skills from simulation to reality │
└──────────────┬──────────────────────────────────┘
│ Real-world feedback (sensors, actions)
▼
┌───────────────────────────────────────────────┐
│ Feedback Loop (Self-Consistency) │
│───────────────────────────────────────────────│
│ • RFM → WFM: Refining prediction accuracy │
│ • WFM → PINNs: Adjusting physical boundaries │
│ • PINNs → RFM: Ensuring physical stability │
└───────────────────────────────────────────────┘


1. PINNs → World Model

• PINNs generate high-quality synthetic data that reflect physical laws.
• This data is used by the world model to learn environmental dynamics and physical interactions.
• Example: Simulating trajectories when a robot pushes an object or reactions during collision to provide training data for the world model.

2. World Model → Robot Foundation Model

• The world model acts as an environment simulator and generates large-scale synthetic data that can be used to train the Robot Foundation Model.
• Through this, the Robot Foundation Model learns generalized control policies for various tasks and environments.
• Example: Using simulation data from the world model, the robot learns how to manipulate objects or avoid obstacles.

3. Overall Flow

• PINNs: Generate synthetic data with guaranteed physical accuracy.
• World Model: Uses PINNs data to simulate environments and generates data required for robot training.
• Robot Foundation Model: Utilizes simulation data from the world model to learn generalized and scalable robot control capabilities.

2. PINNs (Physics-Informed Neural Networks)

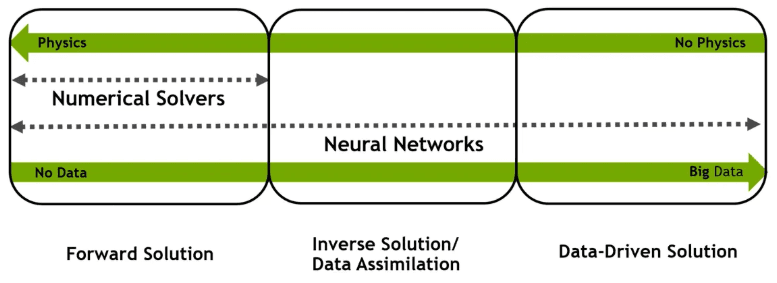
PINNs are neural networks that embed physical laws directly into the loss function to learn functions that satisfy those equations.

Traditional numerical methods (FEM, CFD, etc.) divide space into grid points and repeatedly compute values at each node, whereas PINNs approximate the entire space with a single continuous function.

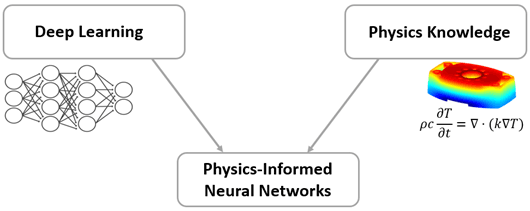
In other words, instead of memorizing values at specific points, the neural network internalizes the form of solutions that satisfy physical equations.

The key is physics-based learning. Because PINNs use PDEs and boundary conditions directly as training objectives, they can be trained even with limited data, offer strong generalization to new boundaries or conditions, reduce computational costs of physical simulations, and generate large-scale physically consistent synthetic data.

• Key Features:
  • Physical equations (e.g., Navier–Stokes, heat transfer) are embedded in the loss function for training.
  • Can be trained using analytical or experimental data.
  • Ensures physically consistent outputs.
  • Provides quality standards for synthetic data generation.
  • Maintains fundamental physical consistency in simulations.
• Direct Objective:
  • Learning solution functions that satisfy physical equations

The most explicit objective of PINNs is:

“To approximate solutions of differential equations not through numerical data, but within the structure of the neural network itself.”

That is, rather than numerically solving PDEs like FEM or CFD, PINNs learn a function that inherently satisfies those equations.

This approach is fundamentally about representation, not repeated computation.

Once trained, a PINN can instantly output a continuous solution at any coordinate, even outside of grid points.

• Deeper Objective:
  • Continuous integration of multi-physics

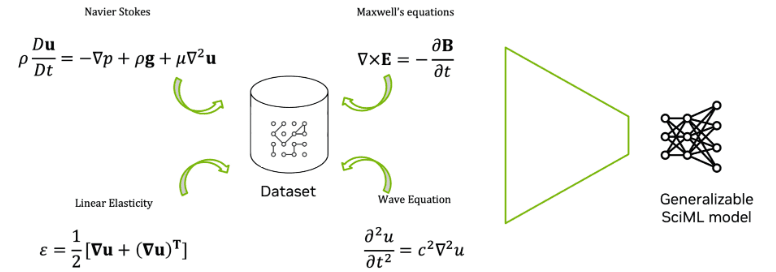
Real-world phenomena almost always occur at the interfaces of multiple physical domains:

• Fluid impacting a solid → interaction of pressure and stress
• Heat transfer → temperature, deformation, and flow are coupled
• Electric current → electromagnetic, thermal, and mechanical stress interactions

Traditional numerical solvers treat domains like fluid, structure, and thermal separately, exchanging values at boundaries — causing discontinuities and instability.

PINNs instead learn all relevant physical equations within a single neural function, jointly approximating fluid PDEs, solid PDEs, and thermal equations in one continuous solution space.

• Representative Models:
  1. NVIDIA Physics NeMo (2023) – GPU-accelerated PINN framework for multi-physics.

1. DeepXDE (Lu et al., 2021) – Open-source PINNs library for solving PDEs like Navier–Stokes, heat equations.

https://github.com/lululxvi/deepxde

1. mathLab/PINA (Haghighat & Juanes, 2025) – PINNs library built on PyTorch Lightning and PyTorch Geometric for scientific machine learning.

https://github.com/mathLab/PINA

3. Extended Architecture of PINNs — NVIDIA PhysicsNeMo + Omniverse

PhysicsNeMo

An open-source physics-ML framework that enables large-scale training and inference for PINNs, FNOs, and other SciML models (Python-based, open-source).

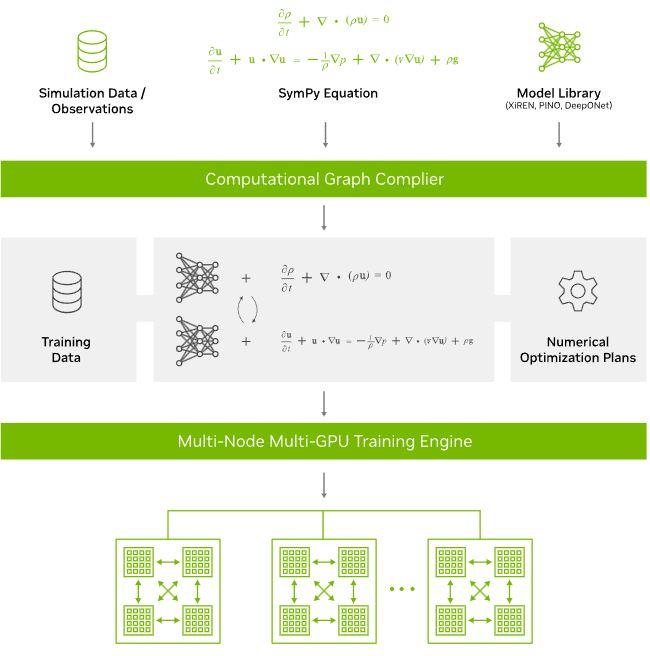
Focused on transforming large physics models into real-time or near real-time predictors.
(Reference: NVIDIA PhysicsNeMo)

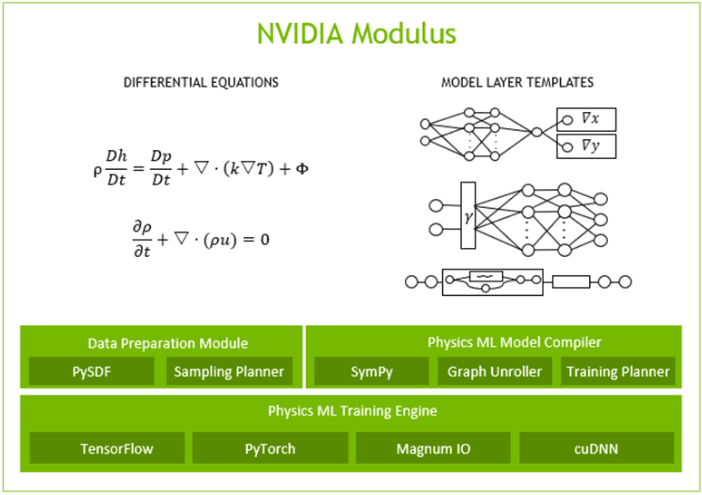
PINNs Documentation & Tutorials

Official documentation provides guidance on how to incorporate PDEs into loss functions and implement physics-informed learning (includes legacy Modulus documentation as well).

(Reference: PINNs in PhysicsNeMo Sym)

CFD / Operator Learning (FNO) Integration

PhysicsNeMo supports Fourier Neural Operator (FNO) implementations to simplify the creation of surrogate models for large-scale fluid or thermal simulations.

(Reference: Transforming CFD Simulations with ML Using NVIDIA PhysicsNeMo)

Omniverse & Cosmos Integration Points

Cosmos (WFM): A World Foundation Model platform for Physical AI (robots, autonomous driving, etc.). Supports synthetic data generation, guardrails, and accelerated pipelines (announced/updated in 2025).

Together with PhysicsNeMo-based physics predictors, Cosmos can be used to construct a physically consistent world model.

(Reference: NVIDIA Launches Cosmos World Foundation Model Platform)

Omniverse Robotics Libraries

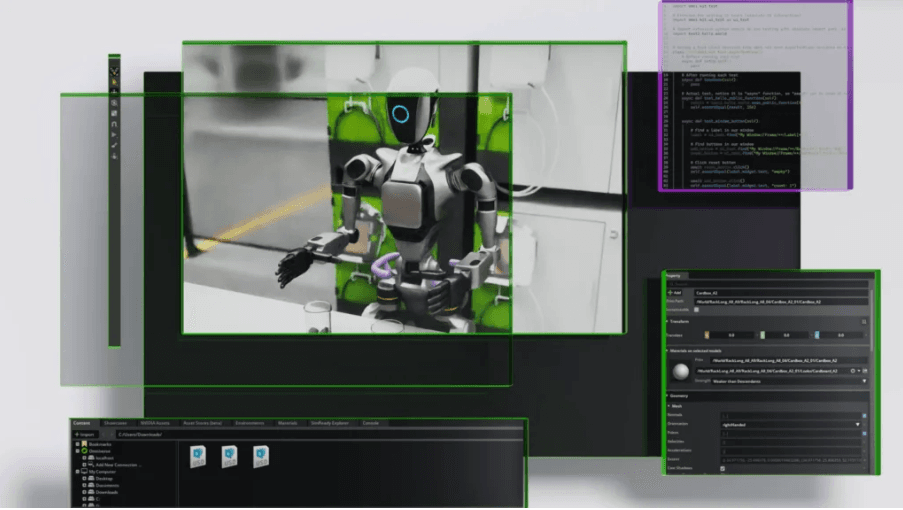
New robotics libraries/tools were released to accelerate workflows from simulation → data generation → training, in conjunction with Cosmos.

(Reference: Developers Build Fast and Reliable Robot Simulations with NVIDIA Omniverse Libraries)

4. Industrial Applications (Applications & Case Studies)

A. Product/Design Acceleration (Engineering)

• Product Development Acceleration: Solving forward/inverse problems using PINN-based physics-ML shortens design and validation cycles (documented in NVIDIA’s official blog).

(Reference: Accelerating Product Development with Physics-Informed Neural Networks and NVIDIA PhysicsNeMo)

• CFD Replacement/Complement: PhysicsNeMo’s FNO-based surrogate models accelerate iterative design/optimization processes.

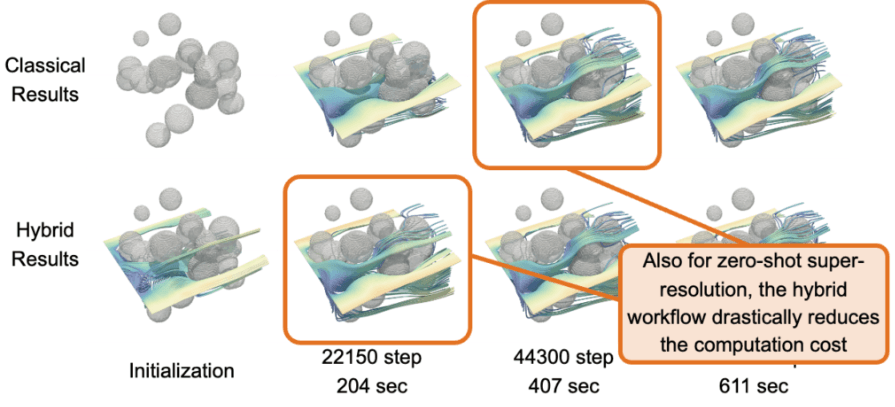
(Reference: Transforming CFD Simulations with ML Using NVIDIA PhysicsNeMo)

B. Digital Twin & Simulation Operations

• Using documented PINN techniques, physics-consistent predictors can be embedded into digital twins on Omniverse for real-time or near real-time responses.

(Reference: Physics Informed Neural Networks in Modulus)

C. Robotics / Autonomous Systems Data Generation

• With Cosmos WFM, various environments and scenarios are synthesized, while PhysicsNeMo/PINNs provide physics-based reactions (collision, flow, heat, etc.) → improving training data quality for robot behavior models.

(Reference: NVIDIA Announces Major Release of Cosmos World Foundation Models and Physical AI Data Tools)
NVIDIA’s Omniverse + Cosmos robotics workflow update formalizes pipelines for simulation, synthetic data generation, and training.

D. Academic/Industrial Hybrid Cases

• PINNs have been used to solve optimization and pathfinding problems, where physical constraints helped discover narrow or unstable solutions that traditional RL/GA algorithms struggle with.

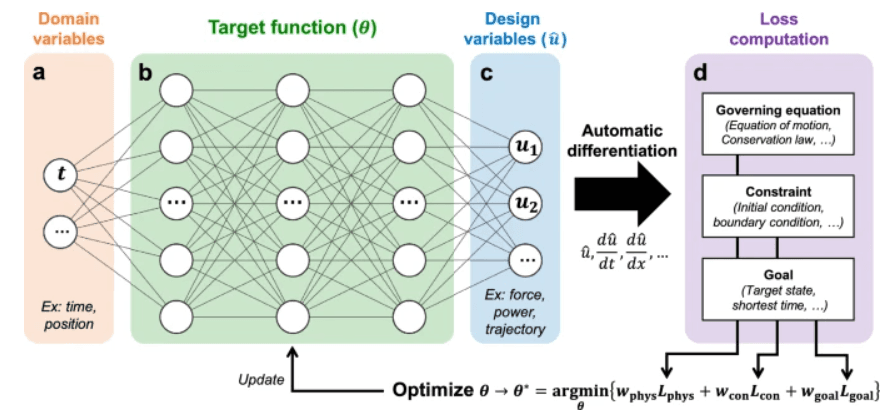
(Reference: Solving real-world optimization tasks using physics-informed neural computing)